Dans cette simulation, on utilise des dés à 6 faces qui représentent des atomes radioactifs. On décide que quand un dé affiche 1, c'est que l'atome qu'il représente est désintégré. Etant donné que chaque face a 1 chance sur 6 de tomber, l'atome a une chance sur 6 de se désintégrer à chaque lancer. Quand un dé est désintégré, on le retire et on relance les autres. On lance donc les dés plusieurs fois, jusqu'à ce qu'ils se soient désintégrés. Pour obtenir des résultats significatifs, on effectue plusieurs séries de lancers, avec lesquels on fait une moyenne.
A l'aide des résultats obtenus, on trace la courbe du nombre d'atomes en fonctions du temps, avec les atomes représentés par les dés et le temps par les lancers. On obtient donc une courbe de décroissance exponentielle que voici:
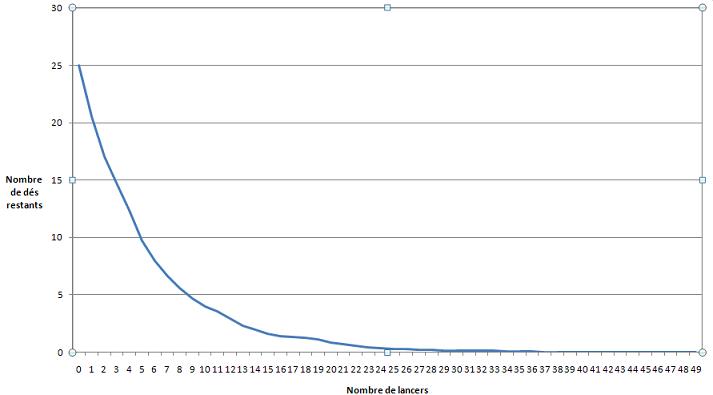
On s’aperçoit qu’au premier lancer, on a une chance sur 6 d’avoir la désintégration, et 5/6 de ne pas en avoir. Au deuxième lancer on a donc 5/6 x 5/6 chances de ne pas avoir de désintégration et ainsi de suite. On se rend donc compte que la probabilité de ne pas s’être désintégré est de (5/6)^n avec n étant le nombre de lancer.
La demi-vie est le moment où la moitié des atomes d'un échantillon radioactif se sont désintégrés.
C'est-à-dire dans le cadre de notre simulation le moment où on a (5/6)x = 0.5.
Pour trouver ce x, on utilise la fonction logarithme.
Donc,
ln((5/6)x)=ln(0,5)
x*ln(5/6)=ln(0,5)
x=ln(0,5)/ln(5/6)
Ce qui nous donne un résultat avoisinant 3,80.
Voici le classeur excel que nous avons codé et qui est à l'origine de la courbe présentée plus tôt. Télécharger.
=SI(ARRONDI.INF(ALEA()*6+1;0)=1;0;1)
Cette fonction, présente dans des cases comme B3 (des feuiles de type "feuil1"), permet de simuler un lancer de dé à six faces: elle génère un nombre aléatoire dans l'intervalle [0;1[, le mutlitple par 6, lui ajoute 1 (pour éviter d'avoir des nombres comme 0) et l'arrondit à l'unité inférieure (pour avoir des nombres entiers). Ensuite, si le résultat est 1, la fonction renvoie 0 (le dé est retiré). Si ce n'est pas le cas, la fonction renvoie 1 (le dé est toujours présent).
=SI(OU(SI(B3=1;ARRONDI.INF(ALEA()*6+1;0);0)=0;SI(B3=1;ARRONDI.INF(ALEA()*6+1;0);0)=1);0;1)
Cette fonctions est présente dans les autres cases. Elle permet de continer à lancer un dé et renvoie un résultat similaire à la fonction décrite précédement. Dans ce cas précis, elle se trouve en B4. Voici d'abord une petite présentation des fonctions booléennes utilisées. La fonction OU, de forme OU(condition à vérifier ; condition à vérifier) renvoie "Vrai" si une des deux conditions à vérifier est vraie. La fonction SI, de forme SI(condition à vérifier ; valeur renvoyée si vrai ; valeur renvoyée si faux) renvoie une valeur dépendant du résultat du test de la condition. Analysons ce code en le découpant par fonctions.
SI(B3=1 ; ARRONDI.INF(ALEA()*6+1;0) ; 0)
On vérifie ici si le dé lancé précédemment s'est désintégré. (ssi B3=0). Si il ne s'est pas désintégré, alors on utilise la première fonction présentée pour générer à nouveau un lancer : ARRONDI.INF(ALEA()*6+1;0) . Si le dé s'est désintégré, alors la fonction renvoie 0. On remarque que cette fonction est utilisée deux fois dans la fonction OU:
OU(SI(B3=1;ARRONDI.INF(ALEA()*6+1;0);0)=0;SI(B3=1;ARRONDI.INF(ALEA()*6+1;0);0)=1)
Cette fonction signifie: "si le dé s'est désintégré précédement, c'est à dire
SI(B3=1 ; ARRONDI.INF(ALEA()*6+1;0) ; 0)= 0"
(Cette condiotion permet de vérifier si il est nécessaire de faire un nouveau lancer ou non. Si elle n'est pas vraie, on effectue alors un lancer)
Ou "si le lancer que j'effectue conduit à une désintégration du dé, c'est à dire
SI(B3=1 ; ARRONDI.INF(ALEA()*6+1;0) ; 0)= 1"
Alors la fonction OUest vraie. (Elle est donc fausse si le précédent lancer et le nouveau lancer du dé ne conduisent pas à une désintégration du dé)
Maintenant, reprenons la fonction entière:
=SI(OU(SI(B3=1;ARRONDI.INF(ALEA()*6+1;0);0)=0;SI(B3=1;ARRONDI.INF(ALEA()*6+1;0);0)=1);0;1)
Ici, la condition à vérifier est la fonction OU décrite précédemment. Traduite en français la condition à vérifier est donc : "le dé s'est désintégré lors du lancer précédent, ou si ce n'est pas le cas, on l'a relancé et il a fait 1".
La valeur à renvoyer si la condition est vérifiée est 0 (le dé est désintégré). Si la condition n'est pas vérifiée, c'est à dire que lors du précédent lancer le dé ne s'était pas désintégré et que en relançant il n'a pas non plus fait 1, on renvoie 1 (le dé n'est pas désintégré).
Dans la colonne AA de chaque feuille "Feuil1", on fait la somme du nombre de dés restants à chaque lancer. Dans la colonne on fait une moyenne de chacune des colonnes AA des "Feuil1", ce qui nous donne une moyenne de nos résultats à chaque lancer, à partir de laquelle on peut tracer une courbe.
Les deux dernières feuiiles contiennent des calculs de statistiques et nottement le calcul de la demi-vie et la courbe de décroissance radioactive.
La radioactivité est une réaction aléatoire et spontanée, dont l'effet principal sur notre organisme concerne l'ADN. Les radiations peuvent provoquer des cancers, et même mener jusqu'à la mort. Cependant, elles peuvent également avoir un effet bénéfique pour notre organisme, par exemple en radiothérapie. Les cellules cancéreuses, contrairement aux cellules saines sont plus sensibles aux radiations qui provoquent chez celles-ci une mutation de la membrane rendant le cytoplasme de la cellule à découvert. Ceci provoque l'assèchement du cytoplasme et la mort de la cellule cancéreuse. Les radiations nucléaires ne sont donc pas uniquement néfastes à notre organisme.
TPE de Lucas Bevilacqua, Florian Bellini, Marinette Simon et Antoine Culot.